

We describe a numerical scheme for solving Maxwell's equations in the frequency domain on a conformal, structured, non-orthogonal, multi-block mesh. Scientific Discovery through Advanced Computing (SciDAC) USDOE Laboratory Directed Research and Development (LDRD) Program OSTI Identifier: 1818754 Grant/Contract Number: AC05-00OR22725 AC02-05CH11231 ERKJ314 ERKJ331 ERKJ345 Resource Type: Journal Article: Accepted Manuscript Journal Name: Set-valued and Variational Analysis Additional Journal Information: Journal Volume: 30 Journal Issue: 2 Journal ID: ISSN 1877-0533 Publisher: Springer Country of Publication: United States Language: English Subject: 97 MATHEMATICS AND COMPUTING compressed sensing joint sparsity strong convergence convex minimization incomplete data infinite vectors mixed norm relaxation forward-backward splitting linear inverse problems parameterized = , (ORNL), Oak Ridge, TN (United States) Sponsoring Org.: USDOE Office of Science (SC), Advanced Scientific Computing Research (ASCR). Publication Date: Research Org.: Oak Ridge National Lab.
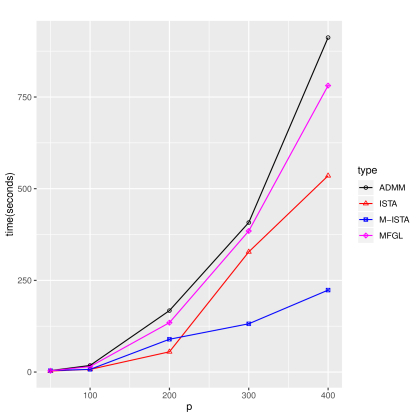
Simon Fraser Univ., Burnaby, BC (Canada).As such, we establish new strong convergence results for the algorithm, in particular when the set of jointly sparse vectors is infinite. However, since the solution matrix possesses infinitely many columns, the arguments of Daubechies et al. This paper discusses the computation of the solutions of linear inverse problems with such relaxation by a forward-backward splitting algorithm. In our case, to take account of the joint sparsity and promote the coupling of nonvanishing components, we employ a convex relaxation approach with mixed norm penalty ℓ 2,1. 46(2), 577613, 2008), which extends the aforementioned work to the joint sparse recovery of finite number of infinite-dimensional vectors. 57(11), 1413–1457, 2004), where the single vector signal can be infinite-dimensional, and (Fornasier and Rauhut, SIAM J.
This is in contrast to the work (Daubechies et al., Pure Appl. We consider the problem of reconstructing an infinite set of sparse, finite-dimensional vectors, that share a common sparsity pattern, from incomplete measurements.


 0 kommentar(er)
0 kommentar(er)
